２月９日（火）の１時間目に４年２組で、井上葉子先生のペア研の授業が行われました。

ペア研の相手は３学期から１年１組担任の貞方先生です。

算数の授業で、「伴って変わる数量」について考える授業でした。

最初に毎時間のルーティンでしょうか。ホームラン問題の提示がありました。井上先生が問題を提示して、学級全員で22人のうち、15人以上が全問正解だったら子どもたちの勝ち、１４人以下だったら、井上先生の勝ちだそうです。

問題の内容を確認したら、さっそく取りかかります。子どもたちは真剣です。

結局、15人の子どもが正解し、見事、子どもたちの勝ちでした。

というわけで、本時の問題に入ります。

今日取り組むのはこんな問題です。

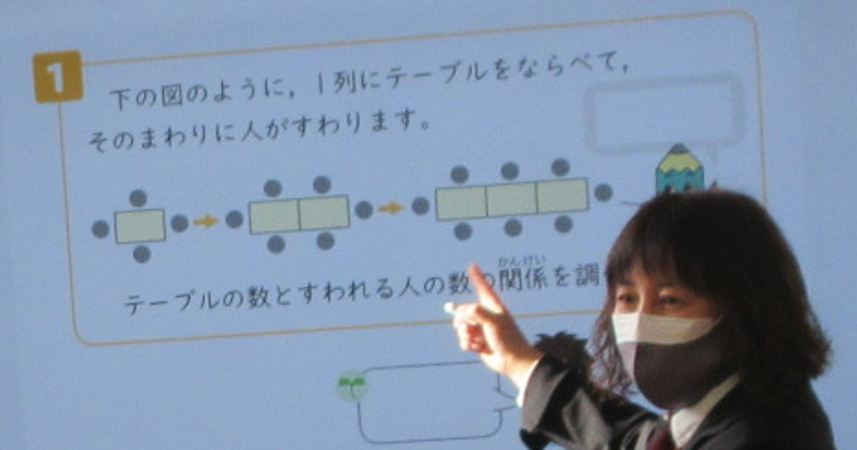
井上先生は子どもたちとやり取りをしながら、めあてを確認していきます。

「今日のめあては何ね？」という問いかけに始まり、子どもたちの中からめあてを引き出していきます。

めあては「表を使ってテーブルの数とすわれる人の数との関係を調べる」となりました。

さっそく、表を使って調べてみます。机が１つ増えると、座れる人は２人ずつ増えていることにたくさんの子どもが気付いているようでした。

 

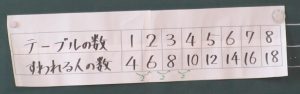
子どもたちは「図をかく」か「増え方のきまりを見つける」と調べられることが分かっているようです。できた子どもたちは考えられるきまりをノートにメモしていました。

そして、自分が考えたきまりを友だちと伝え合ったり、分かっていない友達に教えてあげたりしていました。

子どもたちは、お互いに自分の考えを伝え合い、友達が考えたきまりを自分のものと比べながら興味深く聞いていました。このような活動に生き生きと取り組むことができるのは４年生の素晴らしいところです。

井上先生も子どもたちのやり取りを興味深く聞いています。

「２ずつ増えています！」といったような発言に対して、これまでに学習した「～につれて」「～に伴って」という言葉を用いて、「テーブルの数が一つ増えるに伴って、座れる人の数は２人増える」のように整理し直していました。

他にも、「（テーブルが３つ以上の場合）座れる人の数をテーブルの数で割ると答えは必ず２…余り２になる」といったような考えや、「座れる人の数は必ず偶数になっている」などいろいろな考えが出されていました。

子どもたちの知的好奇心が旺盛であり、考えることを楽しんでいるようにも思えました。

次に、「全員で24人が座りたいときには、テーブルをいくつ準備すればよいですか？」という問いをみんなで考えます。答えが「12」なのか「11」なのかで悩んでいる子どももいるようでした。

 

24人から両端の１人ずつ計２人分を取ると、一つのテーブルに２人ずつ座ることになるから、（24-2）÷2=11でテーブルは11必要という考えでした。なるほどですね。

子どもたちはこの表も式で表せるのではないかということになり、喧々諤々です。子どもたちの好奇心はさらに広がるようです。結局、座れる人の数を△、テーブルの数を〇とすると、（△−２）÷２＝〇　もしくは、〇×２＋２＝△　ということで落ち着きました。

最後に、授業の振り返りをして、終わりました。

子どもたちが考えることを楽しんでいる雰囲気が伝わってくる４年１組の子どもたちでした。

井上先生、お疲れ様でした。